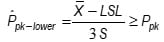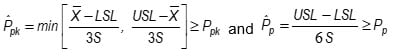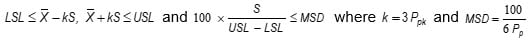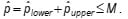STAT-12: Verification/Validation Sampling Plans for Proportion Nonconforming

This procedure provides tables and instructions for selecting sampling plans for FDA process validation and design verification to ensure they are based on a valid statistical rationale. These determine the samples size and acceptance criteria. They make confidence statements like 95% confidence the process or device is more than 99% reliable or conforming. These sampling plans are often referred to as confidence-reliability sampling plans. They are for the statistical property proportion conforming or nonconforming. They require that requirements be established for individual units of product. They apply to design verification (STAT-04), process validation (STAT-03), validation of a pass/fail inspections (STAT-08) and CAPA effectiveness checks (STAT-07).

Appendices

1. Attribute Single and Double Sampling Plans for Proportion Nonconforming
2. Variables Single and Double Sampling Plans for Proportion Nonconforming
3. Selecting Sampling Plans for Proportion Nonconforming using Software
4. Lower Confidence Limit for Percent Conforming—Attribute Data
5. Lower Confidence Limit for Percent Conforming—Variables Data
6. Sampling Plans for Proportion Nonconforming

Highlights

Attribute Sampling Plans

• Appendix F of STAT-12 contains tables like the one shown below for 95%/99% – 95% confidence of more than 99% reliable or conforming. This is equivalent to 95% confidence of less than 1% nonconforming. This table contains attribute single and double sampling plans.

• 95% confidence of more than 99% conformance means there is a 95% chance of rejecting a 99% conforming product/process. 99% conforming is therefore an unacceptable level of quality designed to fail.
• All the above sampling plans, if they pass, allow the same confidence statement to be made. They offer the same protection against a bad product/process passing. They are all equivalent from the customer/regulatory point of view. They differ with respect to their sample sizes and their chances of passing a good product/process. The decision of which confidence statement to use should be based on risk and must be justified. The choice of which sampling plan to use for a given confidence statement is a business decision.
• The AQLs in the above table are nonconformance levels that have a 95% chance of passing the sampling plan. They are useful in deciding which sampling plan to use. Historical data can be used to estimate the nonconformance rate and then matched to the AQL. If historical data is not available, data from similar products or processes can be used. If there is no good estimate of the nonconformance rate, stay away from the top of the table. These are the hardest plans for a good product/process to pass.
• The top plan, n=299, a=0 offers the lowest sample size. It minimizes the sample size. However, it also has the lowest AQL. It maximizes the chance a good product/process will fail.
• The double sampling plans have a first sample size not much greater than the top single sampling plan. They offer a good compromise between sample size and the chance of false rejection of a good product/process. They are generally preferred to the single sampling plans.
• Attribute sampling plans are always applicable. For measurable characteristics, they make no assumption about the underlying distribution of the data. However, they have higher sample sizes. For measurable characteristics, variables sampling plans can be used to dramatically lower the sample size.

Variables Sampling Plans

• Appendix F also contains tables of variables sampling plans. There are separate tables for a one-sided specification and a two-sided specification. When the measurements follow the normal distribution or can be transformed to the normal distribution as described in STAT-18, variables sampling plans can be used to dramatically lower the sample size.

Variables Sampling Plans – One-Sided Specification

• The one-sided specification table is used for both an upper specification limit only and a lower specification limit only. Appendix F of STAT-12 contains tables like the one shown below for 95%/99% – 95% confidence of more than 99% reliable or conforming.

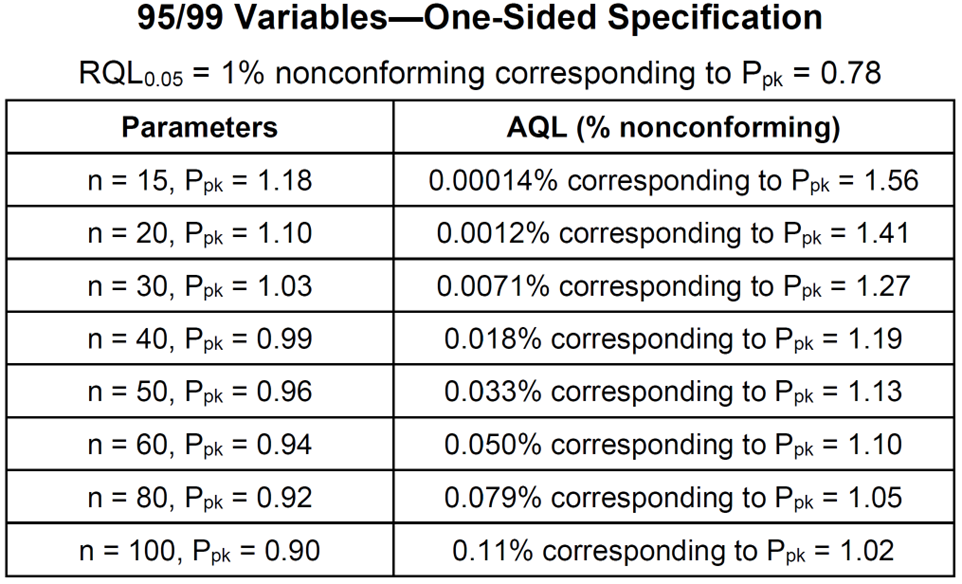
• All the above sampling plans, if they pass, allow the same confidence statement to be made. They offer the same protection against a bad product/process passing. They are all equivalent from the customer/regulatory point of view. They differ with respect to their sample sizes and their chances of passing a good product/process. The decision of which confidence statement to use should be based on risk and must be justified. The choice of which sampling plan to use for a given confidence statement is a business decision.
• The AQLs in the above table are nonconformance levels that have a 95% chance of passing the sampling plan. They are useful in deciding which sampling plan to use. Historical data can be used to estimate the nonconformance rate and then matched to the AQL. If historical data is not available, data from similar products or processes can be used. If there is no good estimate of the nonconformance rate, stay away from the top of the table. These are the hardest plans for a good product/process to pass.
• Confusing to many is that there are multiple ways of writing the acceptance criterion. STAT-12 gives the acceptance criterion for a lower specification limit as:

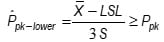
This can be rewritten as

This form corresponds to that of a lower normal tolerance interval and a k-form variables sampling plan in ANSI/ASQ Z1.9. Normal tolerance intervals, k-form variables sampling plans and Ppk-form variables sampling plans are equivalent procedures for the one-sided specification case.

• Suppose n=30 and one wants to construct a 95%/99% 1-sided lower tolerance interval. From a table of k-factors, k=3.064. Dividing by 3 gives 1.02133333. Rounding up gives Ppk = 1.03 per the above table.

Variables Sampling Plans – Two-Sided Specification

• The two-sided specification table is used when upper and lower specification limits both exist. Appendix F of STAT-12 contains tables like the one shown below for 95%/99% – 95% confidence of more than 99% reliable or conforming.

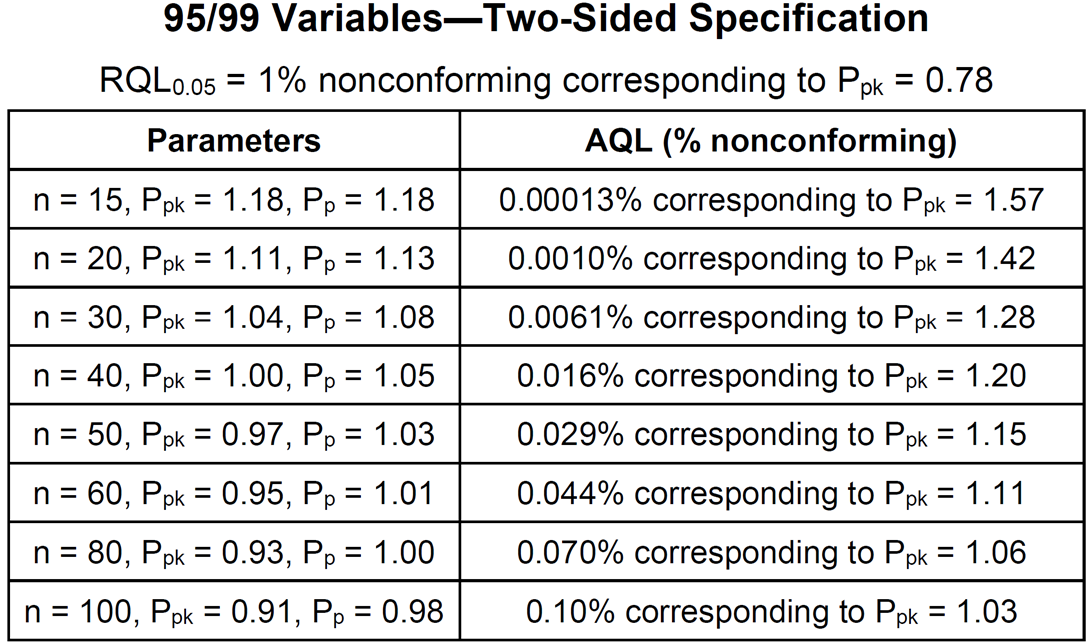
• All the above sampling plans, if they pass, allow the same confidence statement to be made. They offer the same protection against a bad product/process passing. They are all equivalent from the customer/regulatory point of view. They differ with respect to their sample sizes and their chances of passing a good product/process. The decision of which confidence statement to use should be based on risk and must be justified. The choice of which sampling plan to use for a given confidence statement is a business decision.
• The AQLs in the above table are nonconformance levels that have a 95% chance of passing the sampling plan. They are useful in deciding which sampling plan to use. Historical data can be used to estimate the nonconformance rate and then matched to the AQL. If historical data is not available, data from similar products or processes can be used. If there is no good estimate of the nonconformance rate, stay away from the top of the table. These are the hardest plans for a good product/process to pass.
• Confusing to many is that there are both multiple ways of writing the acceptance criteria and different acceptance criteria used. STAT-12 gives the acceptance criteria as

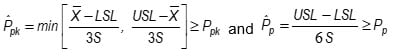
This can be rewritten as

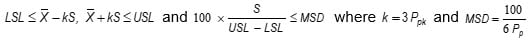
This form corresponds to the k,MSD-form for 2-sided variables sampling plan in ANSI/ASQ Z1.9. The k,MSD-form and Ppk,Pp-form variables sampling plans are equivalent procedures for the two-sided specification case.

• Suppose n=30 and one wants to construct a 95%/99% 2-sided normal tolerance interval. From a table of k-factors k=3.355. Dividing by 3 gives 1.118333. Rounding up gives Ppk = 1.12. This could be used as the acceptance criterion for Ppk by itself. The Ppk acceptance criterion can be relaxed to 1.04 by adding a Pp acceptance criterion of 1.08 per the above table.
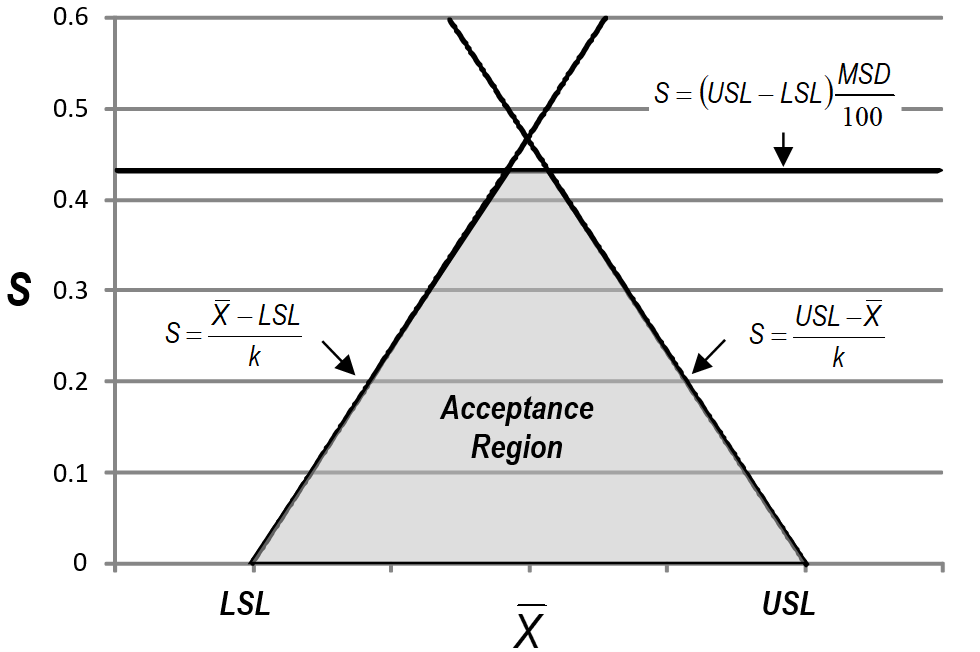
• The difference between a variables sampling plan and a normal tolerance interval can be seen in the plot below. The acceptance criteria for a variables sampling plan is the shaded region below. The acceptance criteria for a 2-sided normal tolerance interval is the triangular region.

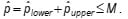
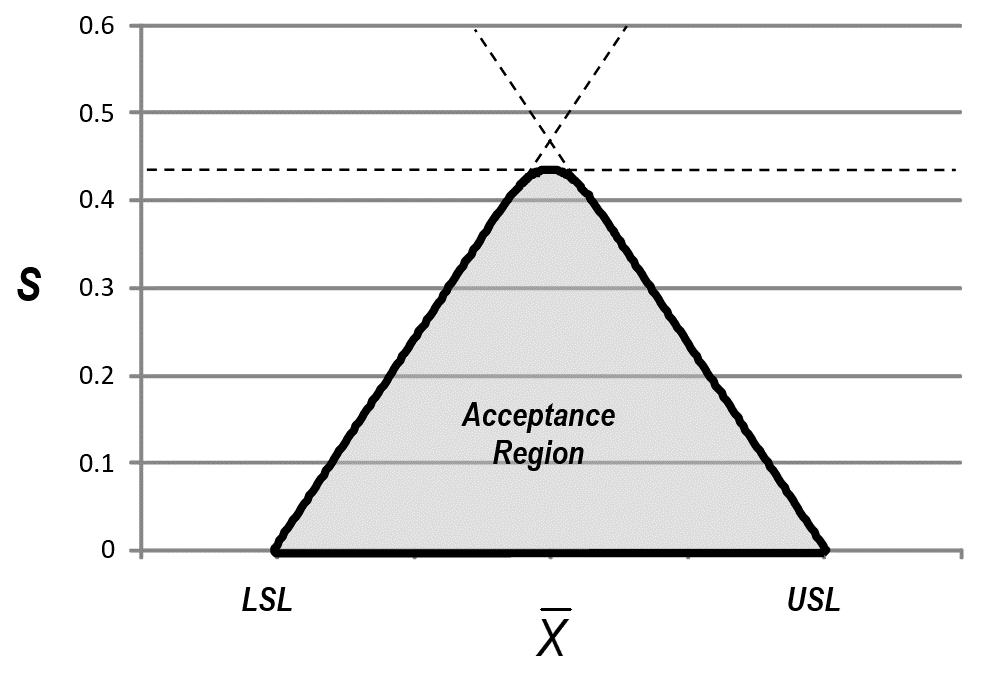
• There is also an M-form for 2-sided variables sampling plans with acceptance criterion based on the estimated percent nonconforming This form is considered the optimal procedure. The acceptance region is shown below. It is more similar to the Ppk,Pp-form acceptance region than the 2-sided normal tolerance interval.

Licenses to the Tables

These tables and all the procedures can be licensed individually or as a group by a company so that they can use them for or as part of their company procedures. This requires paying a 1-time license fee as described at Company Licenses. If your company is using these tables, please make sure they have been properly licensed. Below is a previous version of one of the tables replaced by those in the book of procedures.